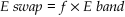THE BEAUTIFUL MATH BEHIND CURVE AMMs PART III: LLAMMA - LENDING-LIQUIDATING AMM ALGORITHM
LLAMMA (Lending-Liquidation AMM Algorithm) is an automated market-making system that continuously “rebalances” a loan’s collateral through an AMM mechanism
Part I: https://x.com/MiradorNews/status/1991119914002776213?s=20
Part II: https://x.com/MiradorNews/status/1993660853162316123?s=20
In the previous Part I and Part II of this series, we explored how Curve approaches AMM design in a very “Curve-liked” way: StableSwap for stable assets and CryptoSwap for volatilized assets. These two AMM were carefully crafted mathematical functions that minimize slippage and maximize capital efficiency across different market regimes.
Part III extends this same mathematical DNA into a completely different frontier: AMM for crvUSD minting and lending markets.
KEY TAKEAWAYS
LLAMMA (Lending-Liquidation AMM Algorithm) is an automated market-making system that continuously “rebalances” a loan’s collateral through an AMM mechanism, which exactly refers to two-way adjustment: liquidating and de-liquidating. Curve enables a new model called soft liquidation through LLAMMA, which is:
A high-sensitivity price curve concentrates liquidity around the oracle and reacts aggressively to price movements, enabling soft, continuous liquidations.
Virtual balances (f, g) shift the AMM price relative to the oracle, creating instant arbitrage incentives that rebalance collateral automatically.
LLAMMA ensures collateral is sold when prices fall and bought back when prices recover, a liquidation engine triggered entirely by an AMM curve.
SECTION 1: CURVE STABLECOIN MECHANISM AND LLAMMA FOR LIQUIDATION
crvUSD is a decentralized stablecoins using crypto assets as collateral, which can be very volatile. Therefore, the stablecoin needs to be overcollateralized, meaning the value of the crypto users have to provide as collateral is higher than the value of the stablecoins they want to mint.
This overcollateralization model works like normal lending and borrowing in DeFi.
For example: Providing 10 ETH as collateral (worth $44,470 at the time of writing), with default number of bands (for liquidation, this will be discussed later), user can borrow (mint) up to $37,972 crvUSD.
In other words, the user must supply at least 115% of the value of the stablecoins they mint as collateral.
This 15% extra buffer is what protects the stablecoin from price swings and keeps it stable.
As other decentralized stablecoins backed by crypto, crvUSD also relies on a liquidation mechanism similar to lending and borrowing platforms. When the value of the collateral drops, liquidation is automatically triggered to prevent the position from slipping into bad debt.
Here is the full working process of Curve’s Stablecoin:
LLAMMA and Liquidation
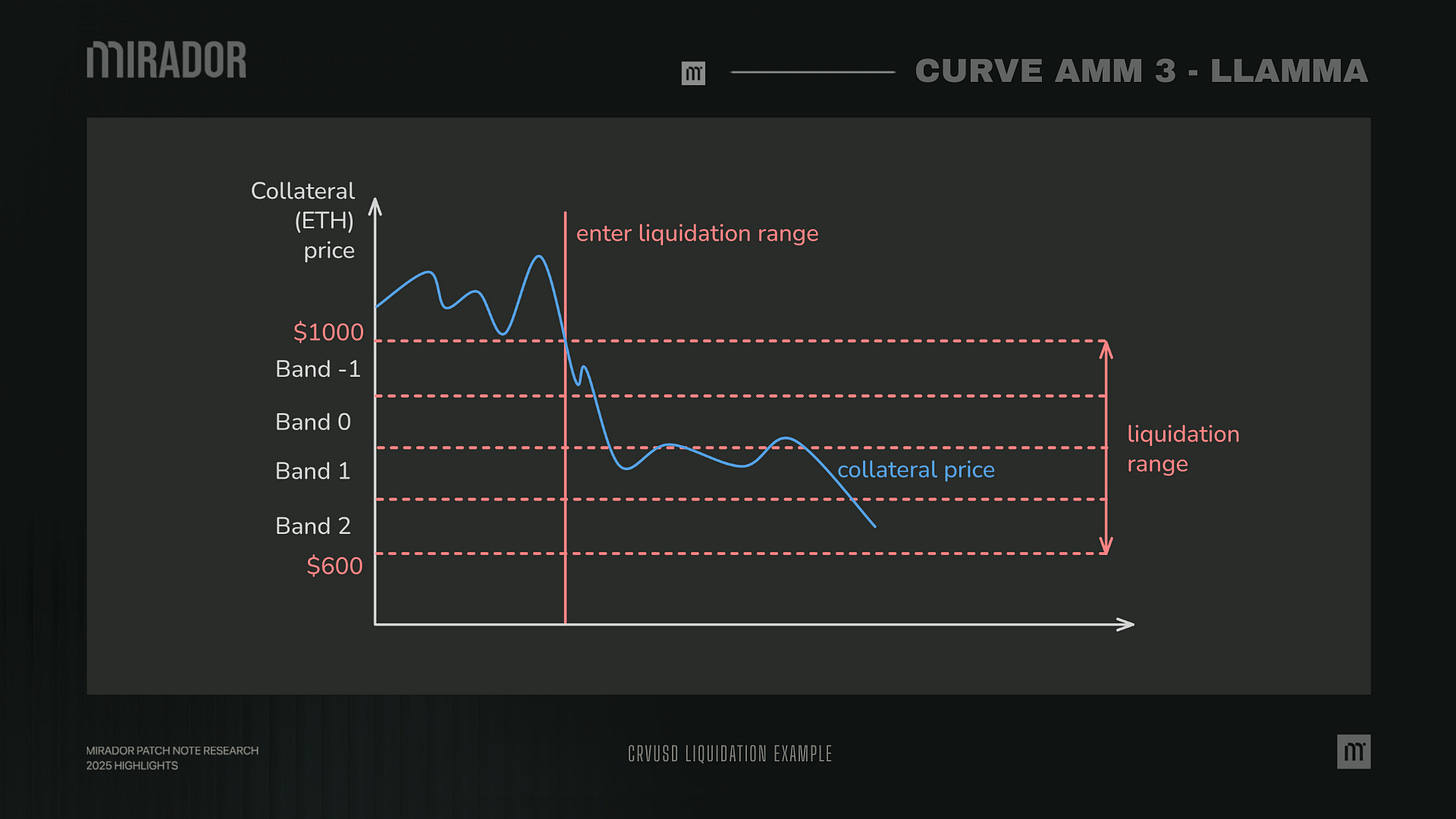
LLAMMA is what makes crvUSD’s liquidiation unique: instead of one-way liquidation, the system uses AMM. Therefore, liquidation turns into rebalancing, which exactly refers to two-way adjustment: liquidating and de-liquidating. Combined with partial liquidation, Curve introduces a new model called soft liquidation.
In general, LLAMMA uses a liquidation range where collateral is continuously adjusted: As prices fall, collateral is gradually converted into crvUSD, and if prices recover, it is converted back into the original asset.
SECTION 2: LLAMMA LIQUIDATION MECHANISM
1/ Collateral price bands and liquidation range
Hard liquidation (or full liquidation) has been pointed out to create a cascading effect, or domino effect, which increases selling pressure for collateral assets and keeps the price continuing to drop. Some protocols have tried to mitigate this by using partial liquidation, where only an enough part of the collateral is liquidated to bring the user’s position back to a safe LTV. This prevents immediate full wipeouts but still results in permanent loss: if the collateral price recovers later, users cannot regain the portion of assets that was already liquidated.
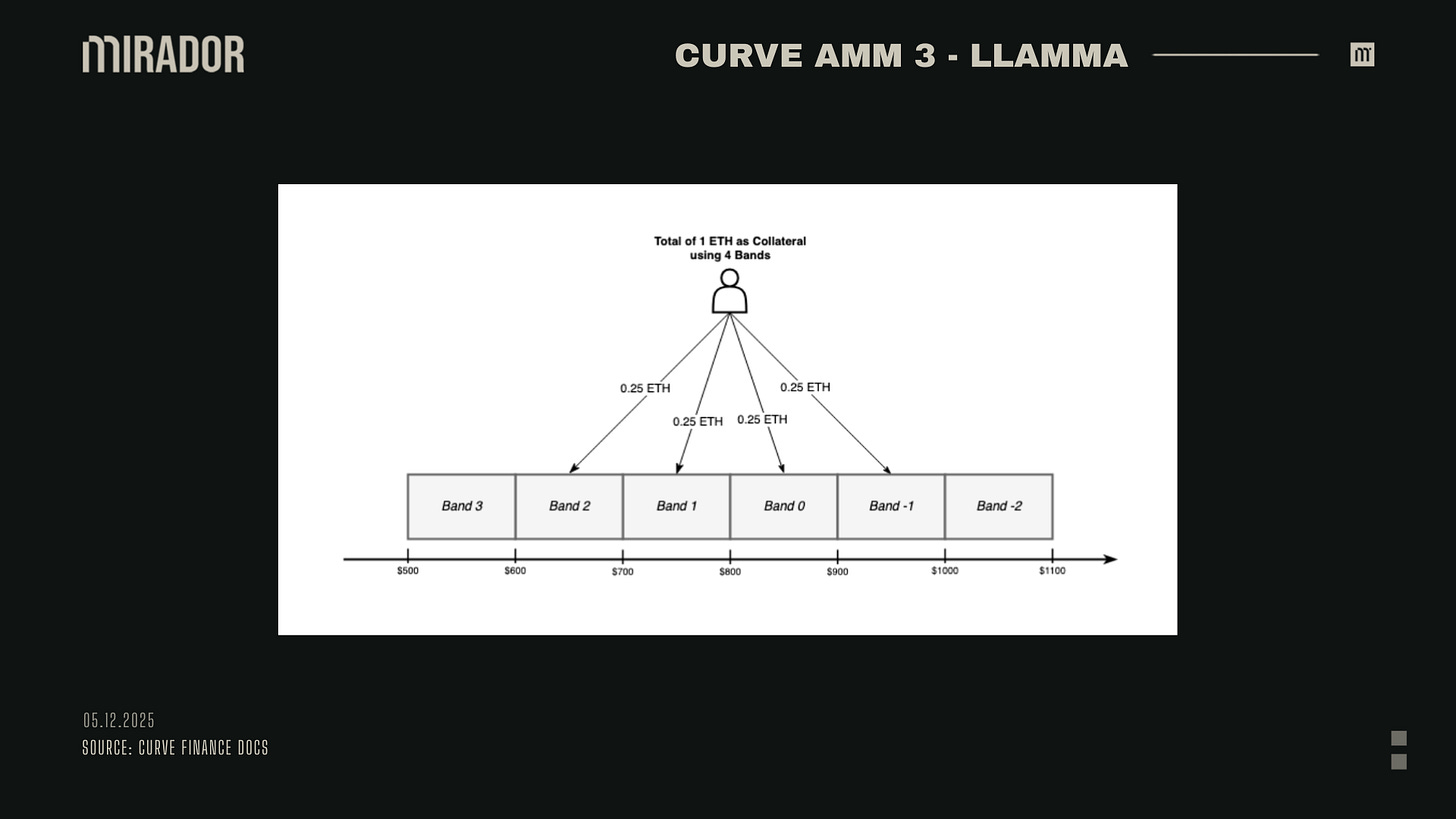
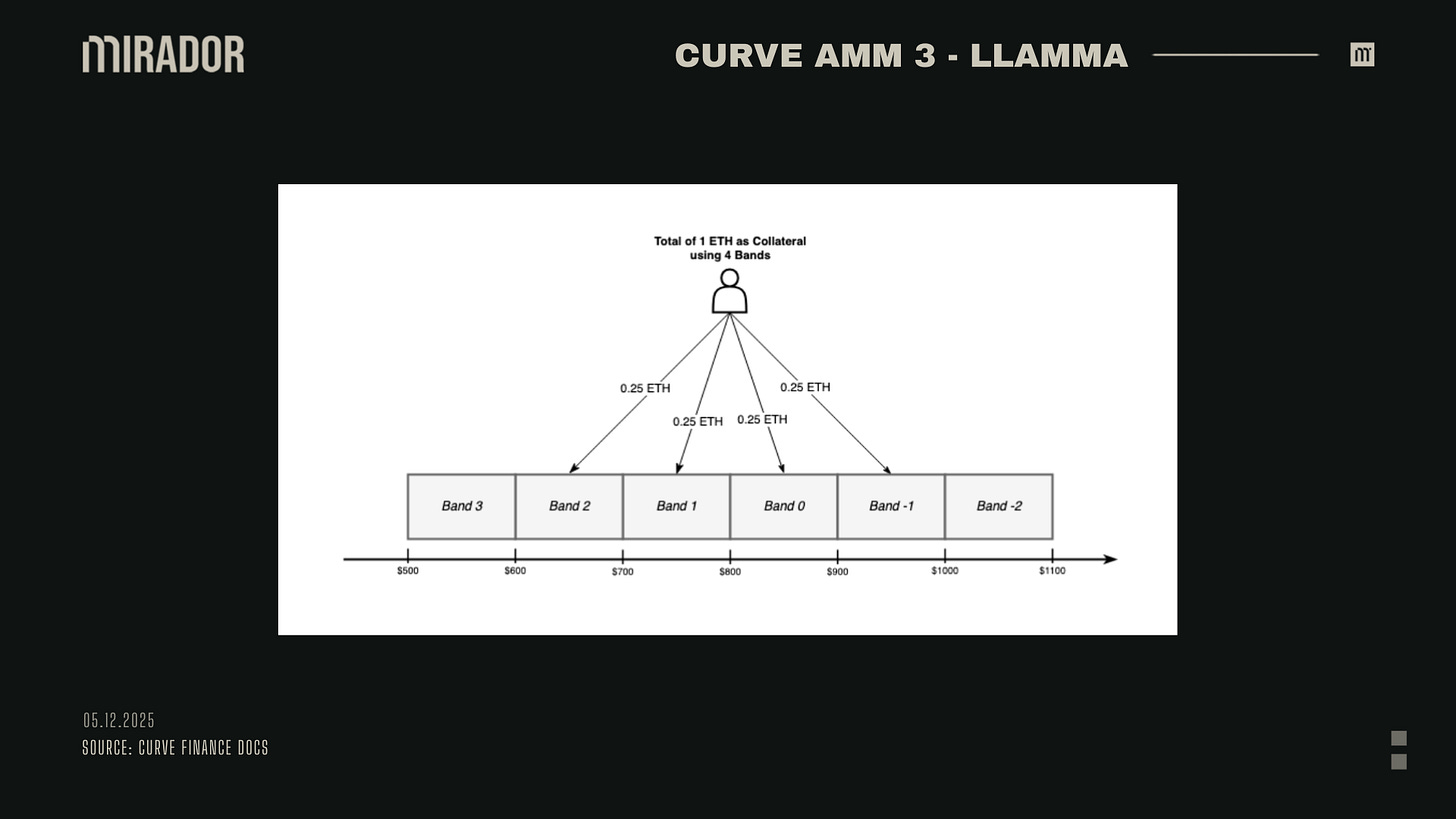
LLAMMA addresses this problem by dividing collateral price range into different bands. Liquidation range of a loan is made of a number of bands (from 4 to 50 bands) that users can choose to store their collateral when creating their positions.
Liquidation range created from bands
In LLAMMA, bands work much like Uniswap V3’s concentrated liquidity “ticks”: Each band represents a price interval where liquidity is placed. When a user opens a loan, their collateral is spread evenly across a chosen number of bands (from 4 up to 50).
Together, these bands form a fixed price grid that defines the liquidation range of the loan.
This feature has been simplified by Curve as the example below:
For example: Alice uses 1 ETH as collateral to mint crvUSD and chooses 4 brands to form liquidation range, her 1 ETH is distributed: 0.25 to band 2, 0.25 ETH to band 1, 0.25 ETH to band 0 and 0.25 to band -1.
Therefore, Alice’s loan liquidation range will be $600 to $1000, which means Alice’s loan enters the liquidation range when the collateral price drops into this range.
2/ Soft liquidation: rebalancing through liquidation and de-liquidation
Partial liquidation
In LLAMMA, collateral is continuously rebalanced whenever its price falls within the liquidation range. When the collateral price drops, LLAMMA sells part of the collateral (any ERC-20, for example, here is ETH) for the borrowed asset (crvUSD), so the loan becomes backed by a mix of ETH and crvUSD.
As long as the collateral price stays above the liquidation range, nothing happens, all the bands remain fully in ETH.
Once the price enters the liquidation range, LLAMMA starts gradually converting ETH into crvUSD, band by band.
For a given band, let:
P↑: top price of the band
P↓: bottom price of the band
Pcurrent : current collateral price
Eband: amount of collateral stored in that band
Eswap: amount of collateral being liquidated (swapped to crvUSD)
When P↓ Pcurrent P↑, we have the formula to calculate the fraction of the band that has been swapped into crvUSD is:
The amount of ETH swapped in that band is:
For example: Returning to the previous example when Alice deposited 1 ETH across 4 bands, each band holds 0.25 ETH (Eband = 0.25)
Now the ETH price drops from $1100 to $650 (Pcurrent = 650).
We have:
Band 1 (1000 → 900): Pcurrent < 900 ⇒ fully swapped → Eswap = 0.25 ETH
Band 2 (900 → 800): Pcurrent < 800 ⇒ fully swapped → Eswap = 0.25 ETH
Band 3 (800 → 700): Pcurrent < 700 ⇒ fully swapped → Eswap = 0.25 ETH
Band 4 (700 → 600): 700 Pcurrent 600
⇒ Total swapped: 0.25+0.25+0.25+0.125=0.875 ETH
So when the price drops to $650, 0.875 ETH has been converted into crvUSD, while the remaining 0.125 ETH stays unconverted in the last band.
As the price keeps falling, the process repeats in the next band, and so on. If the price goes all the way below the lower bound of the liquidation range (below $600), then all ETH is fully converted into crvUSD, and at that point, the loan is completely backed by crvUSD (as long as its health factor stays above 0%, otherwise, it will be hard liquidated - we will discuss this one in the next part).
Deliquidation
De-liquidation is the process of converting crvUSD (created during soft-liquidation) back into the original collateral, such as ETH. For this to happen, the loan must have already been soft-liquidated, otherwise, there is no crvUSD to convert.
When the collateral price falls into the liquidation range, LLAMMA gradually sells ETH for crvUSD, reducing exposure to the falling asset. If the price later rises within that same range, the process is reversed: LLAMMA uses the crvUSD to buy back ETH, restoring exposure to the collateral.
De-liquidation continues until all the crvUSD is converted back into ETH.
Liquidation in LLAMMA works at the band level, not for each user individually. This means if multiple users share the same band, any soft or de-liquidation within that band affects everyone in it, not just a single user.
However, because assets are sold at lower prices and repurchased at higher ones, users may end up with less collateral than before. In this sense, de-liquidation reduces losses compared to hard liquidation but does not guarantee full recovery of the original position.
At its core, both liquidation and de-liquidation are forms of arbitrage: the system sells collateral for crvUSD when the price falls, and buys collateral back with crvUSD when the price rises. This continuous cycle of selling and buying keeps the loan balanced.
To estimate liquidation time, calculate the amount collateral to sell in liquidation and amount collateral to buy in de-liquidation, LLAMMA uses a complicated AMM algorithm with 2 tokens, one is collateral ERC-20, another is crvUSD.
Soft and de-liquidation are triggered when there is difference between two reference prices:
Price_oracle (Po): the collateral price from an external oracle (Curve’s stable pools).
Get_p (P): the internal price calculated by the AMM.
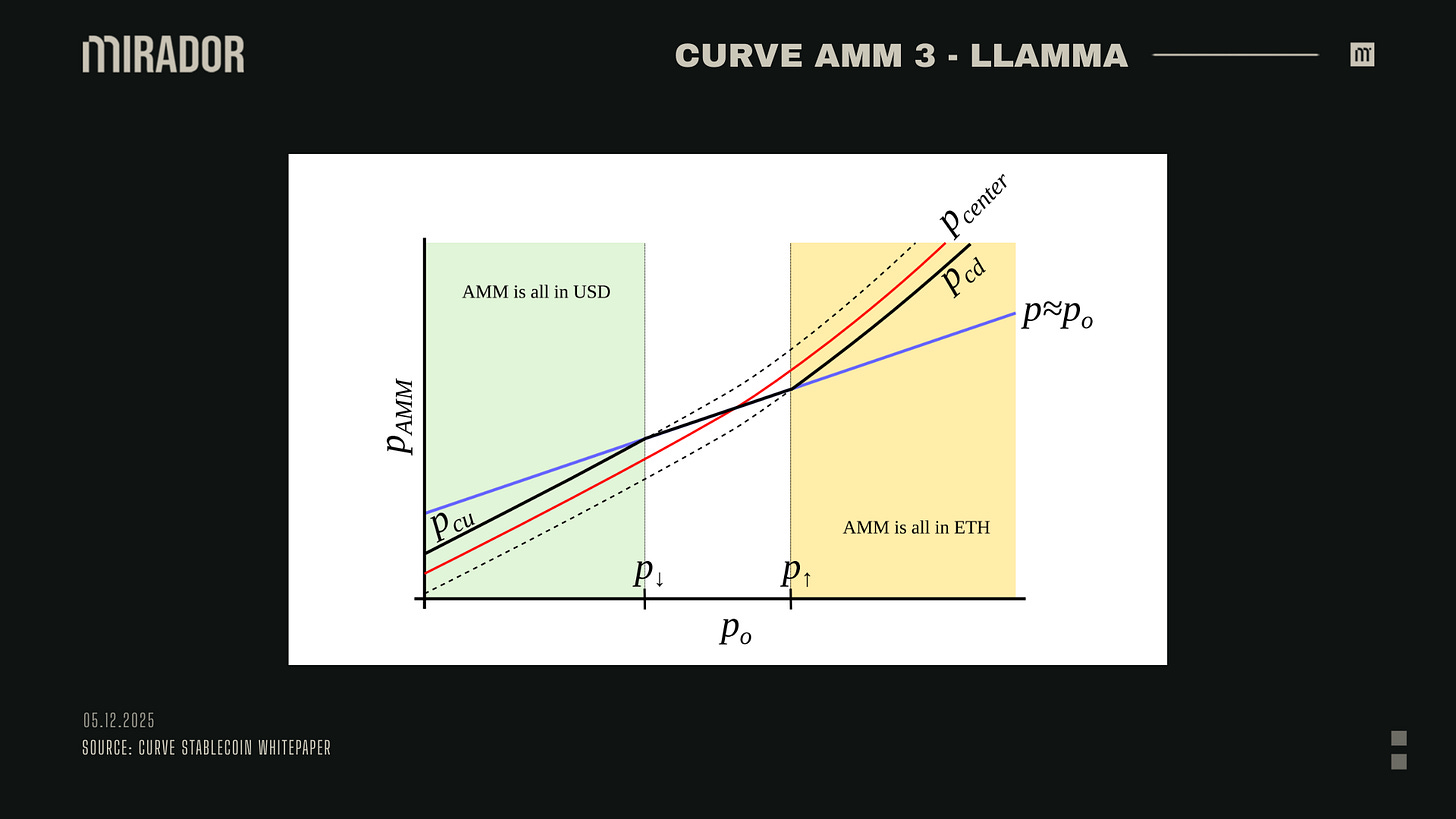
The figure above illustrates the movement of collateral and stablecoin and collateral within a band: with median price Po, P↑ as the top price of the band and P↓ as the bottom price of the band.
This figure illustrates the design goal of LLAMMA’s AMM: to ensure that when the external oracle price Po moves, the AMM price P responds in a faster way.
In practice, this means:
When ETH price (Po) falls gradually to P↓, the AMM gradually shifts ETH fully into USD (crvUSD) and will be full of USD (crvUSD) when Po = P↓ (liquidation).
When ETH price (Po) recovers gradually to P↑, the AMM gradually shifts USD (crvUSD) back into ETH and will be full of ETH when Po = P↑ (de-liquidation).
This response creates a gap between the oracle price and the AMM price, which serves as an arbitrage opportunity. By liquidating, LLAMMA pushes get_p back in line with price_oracle in the arbitrage model. If both prices are equal, no arbitrage is possible and the system stays balanced.
SECTION 3: LLAMMA CONSTRUCTING
1/ Oracle price
The Oracle Price is just the external market price of the collateral. LLAMMA uses this price to decide when to convert collateral ↔ borrow asset (mostly crvUSD) at specific price levels.
Every time LLAMMA fetches a new external price, it smooths the value using EMA (Exponential Moving Average).
EMA works by giving more weight to recent prices and less weight to older ones. This makes the price react smoothly instead of jumping up and down with every tick. The goal is to:
Reduce the impact of sudden, extreme price moves
Make it harder for attackers to manipulate the Oracle Price
What makes LLAMMA different from other AMMs that also use an Oracle Price is the way its AMM price curve reacts to that oracle price.
2/ More sensitive AMM price
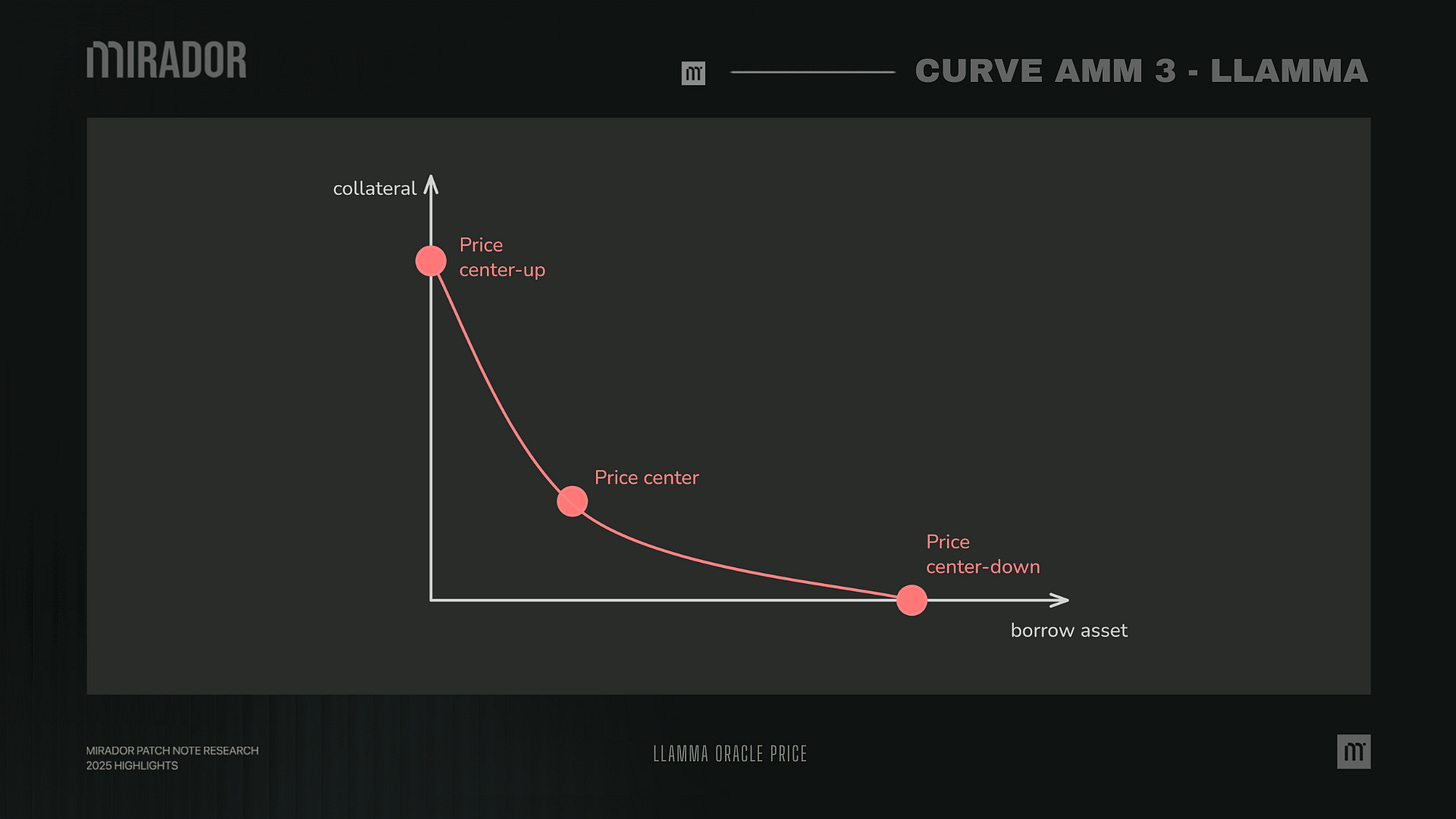
External price (price center) determines a price around which liquidity is formed. AMM supports liquidity concentrated from price center-down to price center-up,
Curve’s aim is to construct an AMM where Pcd and Pcu are such functions of Po that when Po grows, they grow even faster.
In this case, this AMM will be all in ETH when ETH is expensive, and all in USD when ETH is cheap.
If Pcd and Pcu grow linearly with Po, the band moves slowly, it takes a much bigger price change to push the AMM fully to one side. This spreads liquidity more widely, making it less concentrated and causing higher slippage.
If Pcd and Pcu grow faster than linear (steeper), even a small price change shifts the band much more. This makes the AMM convert its assets faster and keeps liquidity highly concentrated around the oracle price, reducing slippage and improving capital efficiency.
For LLAMMA, which needs the AMM to act like a soft liquidator: selling collateral gradually as price falls, and buying it back when price recovers.
If the bands moved only linearly, the AMM would be too slow to react, leaving too much collateral unliquidated when prices drop quickly, increasing bad-debt risk.
With a steeper price curve, LLAMMA “ramps up” faster: it sells more aggressively when price drops, reducing risk, and also buys back faster when price recovers, trying to improve capital efficiency for borrowers.
3/ Constructing AMM for lending invariant
a) Virtual balances and invariant
LLAMMA starts with an AMM that works like Uniswap V3, with:
x = amount of USD (crvUSD) in the band
y = amount of collateral in the band
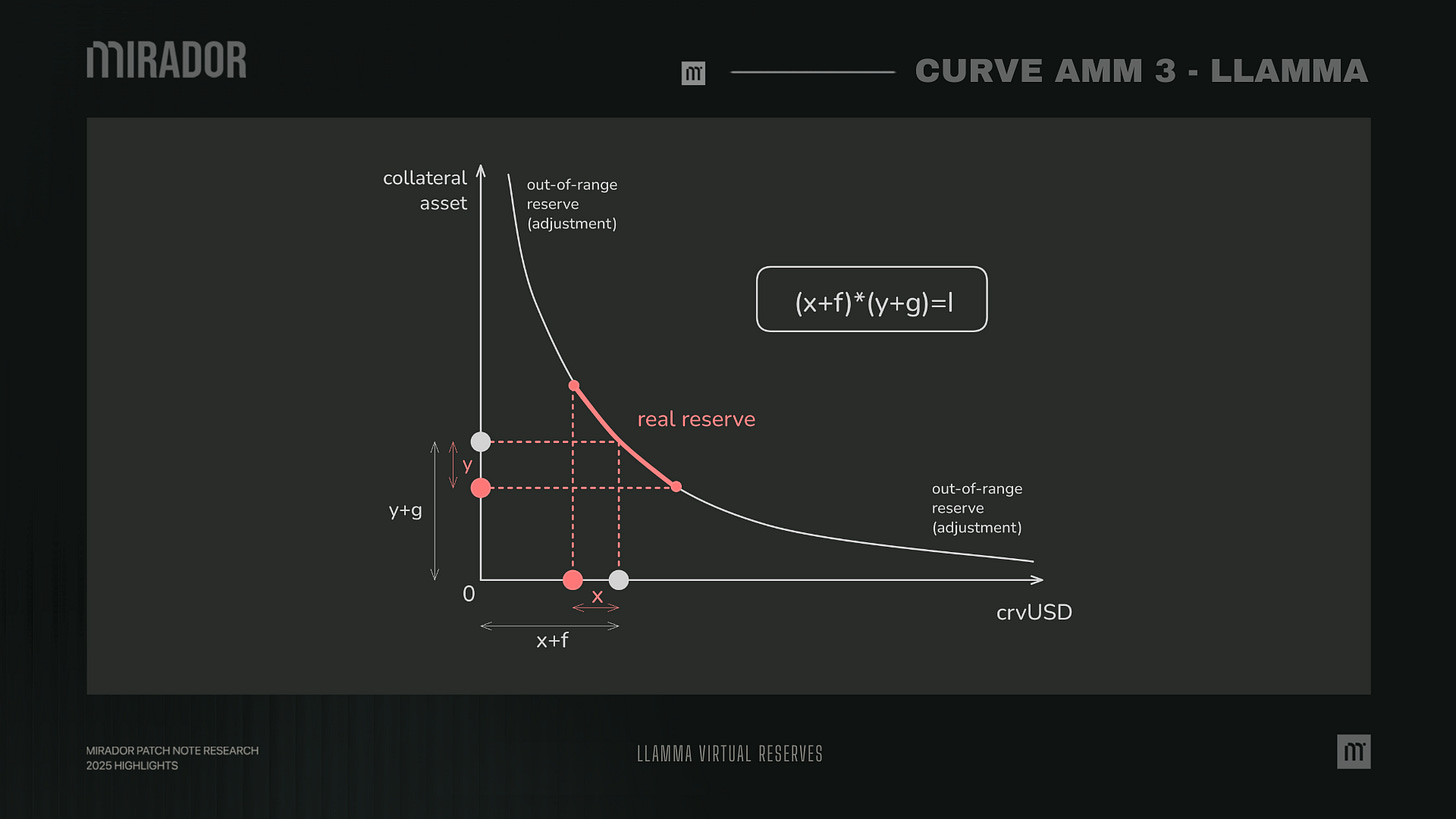
These real reserves are not spread all along the price curve, they are concentrated at a price range, and in LLAMMA, this range is also a band.
To make the curve smooth, they add virtual balances f and g and make a constant product that:
(x+f)(y+g) =I
with:
f acts like USD (crvUSD) out-of-reserve
g acts like collateral out-of-reserve
Together they keep the bonding curve hyperbolic (so trades still follow a constant product invariant). In other words, we have: I=x’*y’ (x’=x+f; y’=y+g) (I is constant)
The key is: f and g change with the oracle price Po. That means the invariant I isn’t truly constant over time, it only stays constant as long as Po does not move. Inside each band (between p↓ and p↑), f and g are fixed.
To calculate f and g value for each band, we have:
With:
A: the ratio that defines the width of each band:
Large A → Narrow band → Liquidity is more concentrated → P_AMM reacts faster
Small A → Wider band → Liquidity is spread out → P_AMM moves more slowly
P↑: the upper price of the band. When the price reaches P↑, the AMM is almost fully converted into ETH for that band.
At that top of the band (P = P↑):
y = y₀
x = 0 (USD is basically drained)
For example: Band price range: P↓=3900; P↑=4100 (USD per ETH).
Real reserves in the band (USD-equivalent):
x = 40,000 (crvUSD in band)
y = 10 (ETH in band)
So the real AMM spot price = x/y=40,000/10=$4,000 (which equals the oracle at start).
Virtual balances initially: f=0, g=0.
Let’s consider 2 scenario of oracle price:
When oracle price goes down to $3,800:
LLAMMA reacts by shrinking virtual USD (f) and increasing virtual collateral (g) inside the band:
New f = 0 (shrunk from 0 → stays 0)
New g = 1 (virtual collateral increases by 1 ETH)
x′ = 40000 + 0 = 40000
y′ = 10 + 1 = 11
PAMM = 40000/11 ≈ $3,636
We have result is:
AMM price ($3,636) is now below the oracle ($3,800).
Arbitrageurs will sell ETH to buy crvUSD on the LLAMMA (they give ETH to the pool and take crvUSD), because they can get crvUSD cheaper from the AMM than on market.
Those trades reduce y’ (ETH in pool) and increase x’ (USD in pool) until PAMM rises back toward the oracle.
The pool returns toward balance; LLAMMA’s virtual changes made the AMM easier to convert ETH to USD when the oracle fell.
When oracle price goes up to $4,200:
LLAMMA reacts by increasing virtual USD (f) and shrinking virtual collateral (g) inside the band:
New f= 4,000 (virtual crvUSD added)
New g = 0 (virtual collateral removed)
x′ = 40,000 + 4,000 = 44,000
y′ = 10 + 0 = 10
PAMM = 44,000/10 = $4,400
We have results is:
AMM price ($4,400) is now above the oracle ($4,200).
Arbitrageurs will sell crvUSD to buy ETH on the AMM (they give crvUSD to the pool and take ETH), because the AMM price for ETH is higher than market, they can buy ETH cheaper elsewhere and sell it to the AMM.
Those arbitrage trades reduce x’ (crvUSD in pool) and increase y’ (ETH in pool) until PAMM drops back toward the oracle.
Net effect: the pool returns toward balance; LLAMMA’s virtual changes made the AMM easier to convert crvUSD to ETH when the oracle rose.
Even if nobody is trading, LLAMMA’s price moves with the oracle automatically, so the pool is always ready for arbitrage to keep balances healthy.
Changing f and g moves the AMM price PAMM = x′/y′ away from the oracle in the same direction; that creates an immediate arbitrage incentive which pushes the real reserves back toward the oracle price. And this is how LLAMMA helps rebalance users’ loans.
CONCLUSION
LLAMMA transforms lending into a continuous, curve-driven mechanism, replacing abrupt liquidations with smooth, mathematically guided rebalancing. By reacting to the oracle through EMA smoothing, steep price bands, and virtual balances that redirect arbitrage incentives, LLAMMA ensures collateral is managed safely and efficiently under all market conditions.
It is the strongest proof yet that a Curve-like AMM can extend far beyond swaps—serving as a foundation for liquidation, stability, and risk management. With LLAMMA, Curve doesn’t just design an AMM; it designs a new class of lending primitive defined entirely by mathematics.
DISCLAIMER
This article is Part III of our Curve AMM series.
Unlike Part I and Part II, which focused on swap-oriented AMMs, this section explores LLAMMA - Curve’s lending–liquidation AMM - a mechanism that uses continuous functions to manage collateral, trigger liquidations smoothly, and stabilize crvUSD.
Because of this shift, we assume readers are already familiar with the foundations of StableSwap and CryptoSwap. Many of the ideas in LLAMMA build directly on the Curve-like AMM principles introduced earlier, so that, we recommend reading the previous parts before moving on to this one.
As LLAMMA involves several moving pieces: oracle smoothing, virtual balances, and band-based price mechanics, we do not avoid the numbers or the math behind it. However, everything will be broken down in a simple and accessible way with clear graphics, so that anyone can follow it.